Raíz cuadrada

En matemáticas se llama raíz cuadrada de un número x, aquel número y tal que multiplicado por sí mismo tenga como producto x. La raíz cuadrada de x se expresa o 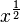. Por ejemplo:

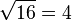, ya que

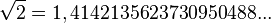
Las raíces cuadradas fueron uno de los primeros desarrollos de las matemáticas, siendo particularmente investigadas durante el periodo pitagórico, cuando el descubrimiento de que raíz de 2 era irracional (inconmensurable) o no expresable como cociente alguno supuso un hito en la matemática de la época.

Posteriormente se fue ampliando la definición de raíz cuadrada. Para los números reales negativos, la generalización de la función raíz cuadrada de éstos da lugar al concepto de los números imaginarios y al cuerpo de los números complejos, algo necesario para que cualquier polinomio tenga sus raíces todas sus raíces (teorema fundamental del álgebra). La diagonalización de matrices también permite el cálculo rápido de la raíz de una matriz.

Inicialmente mostraron su utilidad para la resolución de problemas trigonométricos y geométricos como la diagonal de un cuadrado o el teorema de Pitágoras. Posteriormente fueron ganando utilidad para operar con polinomios y resolver ecuaciones de segundo grado o superior, siendo una de las herramientas matemáticas más elementales hoy en día.
Irracionalidad de las raíces cuadradas [editar]

Las raíces cuadradas de los números enteros que no son cuadrados perfectos son siempre números irracionales, que son números no expresables como el cociente de dos números enteros. Es decir, la raíz cuadrada de un número entero siempre será entero o irracional.

Se puede demostrar fácilmente como sigue:

• n puede ser expresado como el producto de una serie de factores primos elevados a diversos exponentes. De ser todos pares, las propiedades de la potenciación permiten reducir la raíz a un número natural. Sólo si uno o más de los factores tiene un exponente impar la raíz no es natural.
• Si fuera racional se debería poder expresar como con p, q enteros y primos entre sí. Elevando al cuadrado ambas partes se obtiene que lo que es absurdo, pues a un lado queda al menos un factor primo con exponente impar mientras que al otro lado de la igualdad tanto p² como q² se expresan en función de producto de primos elevados a exponentes necesariamente pares

Por una reducción al absurdo llegaron los pitagóricos a la demostración de la irracionalidad de la raíz cuadrada de 2, atribuido a Hipaso, un discípulo de Pitágoras. La idea, contraria a lo esperado en la matemática de entonces supuso una crisis en la filosofía pitagórica.

No obstante, es exactamente la longitud de la diagonal de un cuadrado cuyo lado mide 1, siendo fácil la construcción gráfica de la raíz. Por ello buena parte de la matemática helénica se centró en la geometría aplicada como forma de calcular gráficamente valores como ese. Teodoro de Cirene llegó a la espiral que lleva su nombre que permite representar gráficamente cualquier raíz y posteriormente Euclides llegó a un método más general.

Resolución de raíces cuadradas

Hoy en día existen muchos métodos para poder calcular la raíz cuadrada, habiendo algunos significativos por el hecho de ser a mano y otros por el hecho de ser calculados por una máquina.

Algoritmo manual

Cuando resolvemos la raíz cuadrada con su método de resolución usual podemos ver las partes en las que se divide, aunque las esenciales de esta no tienen por qué aparecer o ser usadas solamente en la operación para ser calculada la raíz cuadrada, según esta imagen podemos ver que las partes de las que se compone son:

1. Radical, es el símbolo que indica que es una raíz cuadrada.
2. Radicando, es el número del que se obtiene la raíz cuadrada.
3. Raíz, es propiamente la raíz cuadrada del radicando.
4. Renglones auxiliares, nos ayudaran a resolver la raíz cuadrada.
5. Resto, es el número final del proceso para resolver la raíz cuadrada.

Los pasos a seguir son estos:

• Paso 1: Se separa el número del radicando (en el ejemplo, 5836.369) en grupos de dos cifras. La separación se hace desde el signo de decimal (si lo hubiera) hacia la derecha y hacia la izquierda. Si del lado de los decimales (a la derecha del punto, es decir 369) no hay un número par de cifras, es evidente que quedaría una suelta: en ese caso, se le añadiría un cero. Si del lado de los enteros (a la izquierda del punto, es decir, 5836) quedara un número suelto, se quedaría así. En la imagen de la derecha podemos ver el número 5836.369 dividido en grupos de dos cifras; después del número 9 se ha agregado un cero (en azul) pues en el lado decimal no puede haber un grupo de una cifra (en el ejemplo, esta separación quedaría así: 58/36.36/90)

• Paso 2: Se busca un número que multiplicado por sí mismo (es decir, elevado al cuadrado) de como resultado el número que coincida o que más se aproxime por debajo al primer grupo de números de la izquierda (en el ejemplo, 58). El resultado no puede ser mayor que 58. Una vez encontrado el número se agrega a la parte de la raíz. En este caso el número sería el 7, porque 7x7 es 49. Otra posibilidad sería 6x6, pero daría 36 (lo que quedaría más alejado de 58) y 8x8, pero daría 64 (lo que excedería a 58).

• Paso 3: El número elegido (7) es el primer resultado de la raíz cuadrada. En el paso anterior lo escribíamos en el cajetín de la derecha. Ahora lo multiplicamos por sí mismo. El resultado (49) se escribe debajo del primer grupo de cifras de la izquierda (58), y se procede a restarlo. El resultado de la resta (58-49) es 9. Una vez obtenido el resultado de la resta, se baja el siguiente grupo de dos cifras (36), con lo que la siguiente cifra de la raíz es ahora la unión del resultado de la resta anterior con las nuevas cifras bajadas (es decir, 936).Para continuar la extracción de la raíz cuadrada multiplicamos por 2 el primer resultado (7) y lo escribimos justo debajo de éste, en el siguiente renglón auxiliar (en la imagen, el 14 está escrito justo debajo del 7, ya que 7x2 es 14).

• Paso 4: En este paso hay que encontrar un número n que, añadido a 14, y multiplicado por ese mismo n, de como resultado un número igual o inferior a 936. Es decir, podría ser 141x1, 142x2, 143x3... y así hasta 149x9. Muchas veces se utiliza el procedimiento de tanteo para hallar ese número, si bien se puede emplear el método de dividir las primeras dos cifras del residuo (93) entre el número del renglón auxiliar (14). La primera cifra del resultado que no sea cero, aunque sea un decimal, es, generalmente, la que buscamos. El resultado se agrega al número de la raíz y al del renglón auxiliar. En este caso 93 dividido entre 14 es 6. De manera que la operación buscada es 146x6= 876 (operación que añadimos en el renglón auxiliar). El siguiente resultado de la raíz cuadrada es 6. También procedemos a anotarlo en el radicando.

• Paso 5: El procedimiento a seguir es el mismo que anteriormente. El resultado de la operación anterior (876) se coloca debajo del número procedente de la resta anterior (936) y se restan. Al resultado de la resta (60) se le añade el siguiente grupo de cifras del radical (en este caso, 36). Si el siguiente grupo está después del punto decimal se agrega un punto decimal al número de la raíz. El nuevo número obtenido es 6036.

• Paso 6: Retomamos el procedimiento del paso 4. La cifra de la raíz (76) se multiplica por dos (resultando 152). Buscamos un número que añadido a 152 y multiplicado por ese mismo número nos dé una cantidad aproximada a 6036. Sería, por tanto, 1521x1, 1522x2, 1523x3, etc. Lo podemos hacer por tanteo, o por el procedimiento de dividir en este caso, las tres primeras cifras de la raíz por las tres primeras cifras de la línea auxiliar (nótese que antes eran las dos primeras cifras), es decir, 603/152 (el número buscado es 3, ya que el resultado es 3.9 y hemos dicho que la cifra que debemos tomar es la primera). La operación a realizar es, por tanto, 1523x3. El resultado (4569) se coloca bajo el último resto y se procede a hallar la diferencia (que es 1467). Una vez realizada la resta se baja el siguiente grupo de cifras y se continúa el proceso. Obsérvese que el número a dividir entre renglón auxiliar y residuo va aumentado.

• Paso 7: Se continúa el mismo proceso, la raíz se vuelve a multiplicar por dos (ignorando el punto de los decimales). El resultado de la multiplicación se agrega al tercer renglón auxiliar, se vuelven a dividir los primeros cuatro números del residuo (1467) entre el resultado de la multiplicación (152), y se obtiene la siguiente cifra para la raíz y el número del renglón auxiliar (9). Dicha cifra se multiplica por el número del tercer renglón auxiliar y se le resta al tercer residuo. Se continua el proceso, si ya no hay más cifras la raíz ha terminado. En este caso, 76.3 se multiplica por 2 como 763 (763x2) que nos da un resultado de 1526. La cifra resultante es 14679 (nótese que son las primeras cuatro cifras, cuando antes eran las tres primeras), y se divide entre 1526, lo que nos da un resultado de 0.9 (como decíamos antes, se toma el primer número aunque sea decimal, por lo tanto, la cifra buscada es 9). El nueve se agrega en el renglón de la raíz y el tercer renglón auxiliar, y se multiplica 9 por 15269, lo que da un resultado de 137421, esta cifra se le resta a 146790 y nos da un resultado de 9369.

La raíz cuadrada de 5836.369 es 76.39, con un residuo de 9369. Recordemos que el cero es sólo un auxiliar. Es importante señalar también que la operación anterior utilizada como ejemplo no está completa. Si la continuáramos daría como resultado 76.396132 (con seis decimales).

Algoritmos para máquinas

Calculadoras, hojas de cálculo y otros softwares también se usan con frecuencia para calcular raices cuadradas. Los programas de software ponen típicamente buenas rutinas en su ejecución para computar la función exponencial y el logaritmo natural o logaritmo, computándose después la raíz cuadrada de x usando la identidad:

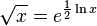o

Se explota la misma identidad al computar raíces cuadradas con tablas de logaritmos o reglas de cálculo...